How To Draw Roc Curve In Numbers

Understanding the ROC Bend and AUC

These binary nomenclature functioning measures go manus-in-manus — allow'southward explore.

Photo by Madeline Pere on Unsplash

The ROC Curve

The receiver operating characteristic (ROC) curve is oftentimes used for evaluating the functioning of binary classification algorithms. It provides a graphical representation of a classifier'south performance, rather than a single value like virtually other metrics.

Start, allow'southward plant that in binary classification, there are four possible outcomes for a test prediction: true positive, false positive, true negative, and false negative.

Defoliation matrix structure for binary classification problems

The ROC curve is produced by calculating and plotting the true positive rate against the false positive rate for a unmarried classifier at a variety of thresholds. For example, in logistic regression, the threshold would exist the predicted probability of an observation belonging to the positive form. Normally in logistic regression, if an observation is predicted to exist positive at > 0.v probability, it is labeled as positive. However, nosotros could really choose whatsoever threshold betwixt 0 and 1 (0.1, 0.3, 0.vi, 0.99, etc.) — and ROC curves help united states of america visualize how these choices bear upon classifier performance.

The true positive charge per unit, or sensitivity, can be represented every bit:

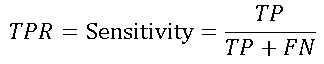
where TP is the number of true positives and FN is the number of false negatives. The true positive rate is a measure of the probability that an actual positive instance volition be classified every bit positive.

The false positive charge per unit, or 1 — specificity, can be written as:

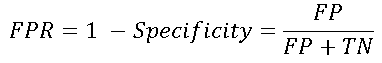
where FP is the number of false positives and TN is the number of true negatives. The false positive rate is substantially a measure out of how oftentimes a "faux alarm" will occur — or, how often an actual negative case will be classified equally positive.

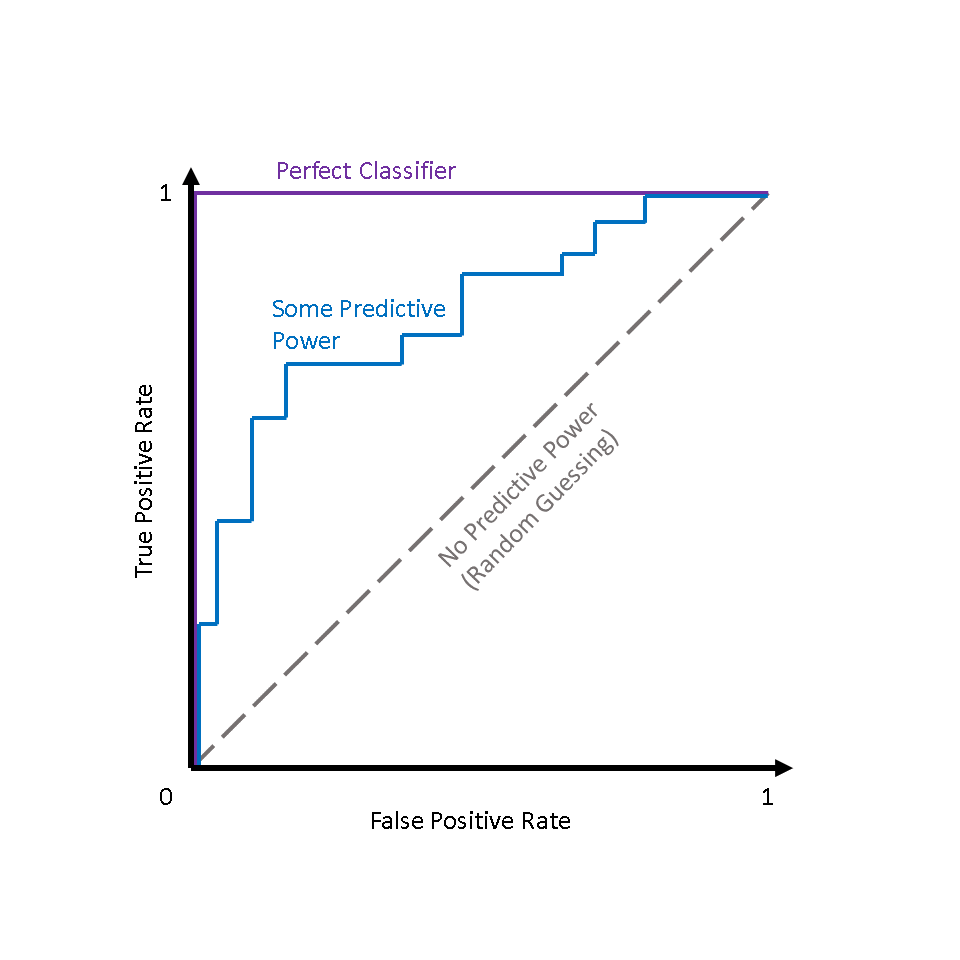
Figure ane demonstrates how some theoretical classifiers would plot on an ROC curve. The grayness dotted line represents a classifier that is no better than random guessing — this volition plot every bit a diagonal line. The purple line represents a perfect classifier — one with a truthful positive rate of 100% and a false positive rate of 0%. Nearly all real-world examples will fall somewhere between these two lines — not perfect, merely providing more than predictive power than random guessing. Typically, what we're looking for is a classifier that maintains a high truthful positive rate while besides having a depression faux positive charge per unit — this ideal classifier would "hug" the upper left corner of Figure one, much like the purple line.

Fig. one — Some theoretical ROC curves

AUC

While it is useful to visualize a classifier's ROC curve, in many cases we can eddy this information down to a unmarried metric — the AUC.

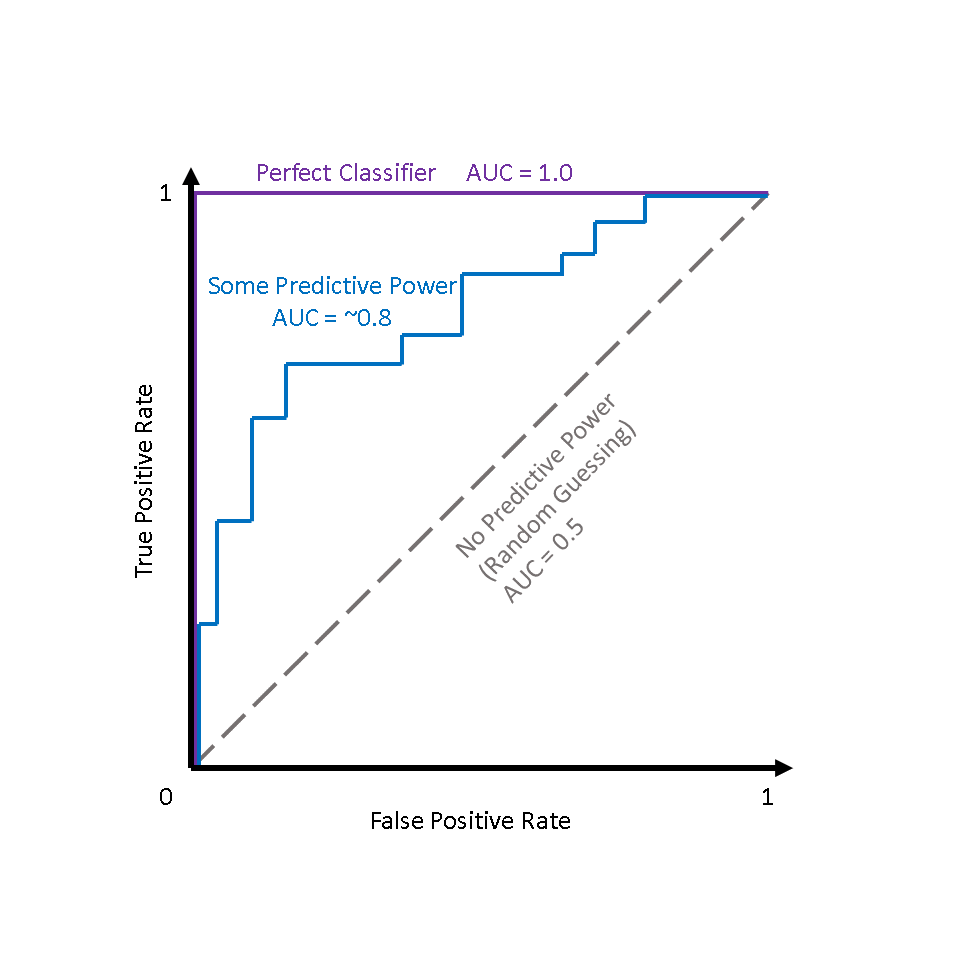
AUC stands for area under the (ROC) curve. Generally, the college the AUC score, the better a classifier performs for the given chore.

Figure 2 shows that for a classifier with no predictive power (i.due east., random guessing), AUC = 0.5, and for a perfect classifier, AUC = 1.0. Most classifiers will fall between 0.5 and one.0, with the rare exception being a classifier performs worse than random guessing (AUC < 0.5).

Fig. 2 — Theoretical ROC curves with AUC scores

Why utilize ROC Curves?

One advantage presented past ROC curves is that they assist us in finding a classification threshold that suits our specific problem.

For example, if we were evaluating an email spam classifier, we would desire the simulated positive charge per unit to be actually, actually low. We wouldn't desire someone to lose an important email to the spam filter only considering our algorithm was too aggressive. We would probably even allow a off-white amount of actual spam emails (truthful positives) through the filter just to make sure that no important emails were lost.

On the other hand, if our classifier is predicting whether someone has a last disease, nosotros might be ok with a higher number of fake positives (incorrectly diagnosing the disease), merely to brand sure that we don't miss any true positives (people who actually have the illness).

Additionally, ROC curves and AUC scores also permit us to compare the operation of different classifiers for the same problem.

Case: Heart Illness Prediction

To demonstrate how the ROC curve is constructed in practice, I'one thousand going to work with the Center Disease UCI data set up in Python. The data set has 14 attributes, 303 observations, and is typically used to predict whether a patient has middle illness based on the other 13 attributes, which include age, sexual practice, cholesterol level, and other measurements.

Imports & Loading Data

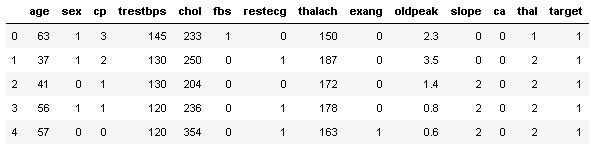
Train-Test Split

For this analysis, I'll use a standard 75% — 25% train-test split.

Logistic Regression Classifier

Before I write a function to calculate false positive and true positive rate, I'll fit a vanilla Logistic Regression classifier on the training data, and brand predictions on the test set.

Calculating Truthful Positive Rate and Faux Positive Rate

Now that I have examination predictions, I can write a part to calculate the true positive charge per unit and fake positive rate. This is a disquisitional pace, equally these are the two variables needed to produce the ROC curve.

          (0.6923076923076923, 0.1891891891891892)        

The exam shows that the function appears to be working — a true positive rate of 69% and a false positive rate of 19% are perfectly reasonable results.

Exploring varying thresholds

To obtain the ROC curve, I demand more one pair of truthful positive/fake positive rates. I need to vary the threshold probability that the Logistic Regression classifier uses to predict whether a patient has center affliction (target=one) or doesn't (target=0). Remember, while Logistic Regression is used to assign a form label, what information technology's actually doing is determining the probability that an observation belongs to a specific course. In a typical binary classification problem, an observation must accept a probability of > 0.5 to be assigned to the positive class. Withal, in this instance, I will vary that threshold probability value incrementally from 0 to 1. This volition result in the ranges of true positive rates and false positive rates that let me to build the ROC curve.

In the code blocks below, I obtain these true positive rates and false positive rates across a range of threshold probability values. For comparing, I use logistic regression with (1) no regularization and (two) L2 regularization.

Plotting the ROC Curves

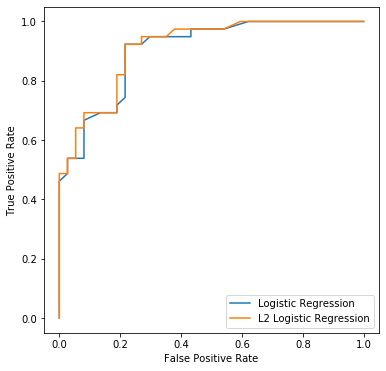
Both versions of the logistic regression classifier seem to do a pretty good job, merely the L2 regularized version appears to perform slightly better.

Calculating AUC scores

sklearn has an auc() function, which I'll brand use of hither to calculate the AUC scores for both versions of the classifier. auc() takes in the true positive and false positive rates nosotros previously calculated, and returns the AUC score.

          Logistic Regression (No reg.) AUC 0.902979902979903
Logistic Regression (L2 reg.) AUC 0.9116424116424116        

As expected, the classifiers both have similar AUC scores, with the L2 regularized version performing slightly better.

ROC curves and AUC the easy way

Now that we've had fun plotting these ROC curves from scratch, you'll be relieved to know that there is a much, much easier way. sklearn'southward plot_roc_curve() function can efficiently plot ROC curves using only a fitted classifier and test data equally input. These plots conveniently include the AUC score besides.

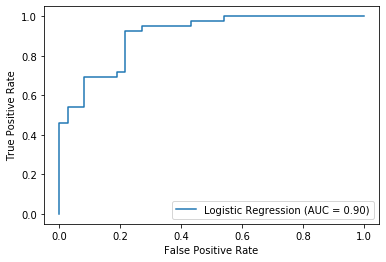
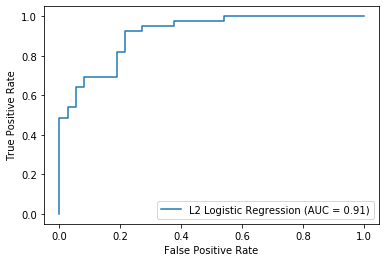
Closing

If y'all've fabricated it this far, thanks for reading! I plant information technology a valuable practice to inefficiently create my own ROC curves in Python, and I hope you gained something from post-obit along.

Some helpful references on ROC and AUC:

Source: https://towardsdatascience.com/understanding-the-roc-curve-and-auc-dd4f9a192ecb

Posted by: dipalmadight1942.blogspot.com

Share this post